1.通过不同路径重力做功的分析,归纳出重力做功与路径无关的特点。　 2.理解重力势能的表达式,通过重力做功与重力势能变化的关系体会功能关系。　 3.知道重力势能的大小与参考平面的选取有关,即重力势能具有相对性。　 4.理解弹性势能,知道影响弹性势能大小的相关因素。

一、重力做的功
        知识梳理
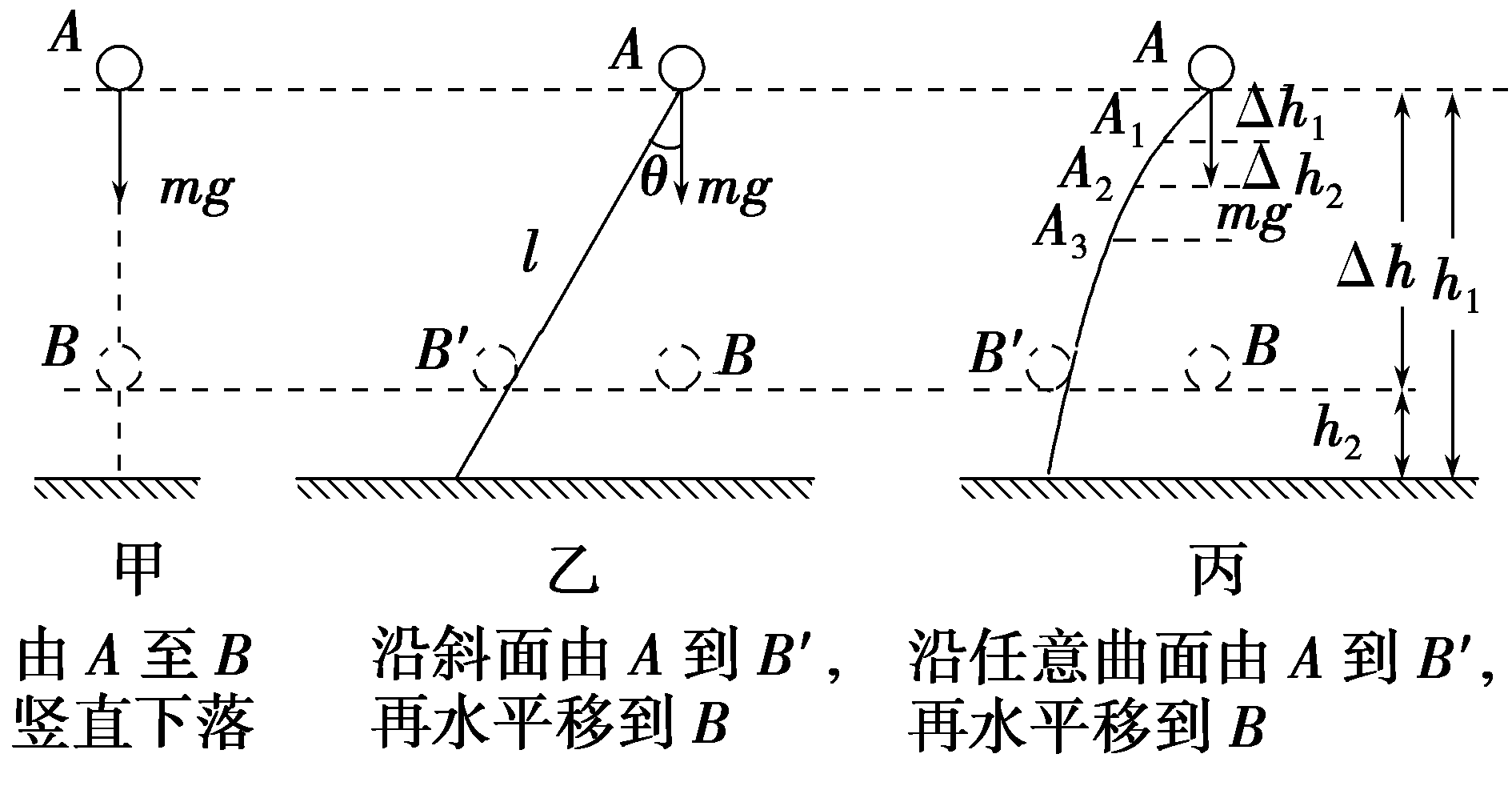
1．重力做功的表达式：W_G＝mgΔh＝mgh₁－mgh₂,其中h₁、h₂分别表示物体起点和终点的高度。
2．重力做功的特点：物体运动时,重力对它做的功只跟它的起点和终点的位置有关,而跟物体运动的路径无关。
总结：
1．重力做功只与重力和物体高度变化有关,与运动路径无关。
2．物体下降时重力做正功,W_G＝mgh；物体上升时重力做负功,W_G＝－mgh。
3．重力做功的特点可推广到任一恒力做功,即恒力做功的特点是：与物体运动的具体路径无关,恒力做的功等于力与在力的方向上的位移大小的乘积,跟初、末位置有关。
二、重力势能　重力势能的相对性
        【一】知识梳理
1．重力势能
(1)定义：我们把mgh叫作物体的重力势能,常用E_p表示。
(2)表达式：E_p＝mgh。
(3)单位：在国际单位制中是焦耳,符号为J。1 J＝1 kg·m·s－2·m＝1 N·m。
(4)重力做功与重力势能变化的关系
①表达式：W_G＝E_p1－E_p2。
②两种情况
当物体由高处运动到低处时,重力做正功,重力势能减少,即W_G＞0,E_p1＞E_p2。
当物体由低处运动到高处时,重力做负功,重力势能增加,即W_G＜0,E_p1＜E_p2。重力做负功也可以说成物体克服重力做功。
2．重力势能的相对性
(1)参考平面：物体的重力势能总是相对于某一水平面来说的,这个水平面叫作参考平面。在参考平面上,物体的重力势能取为0。
(2)重力势能的相对性
选择不同的参考平面,物体重力势能的数值是不同的。
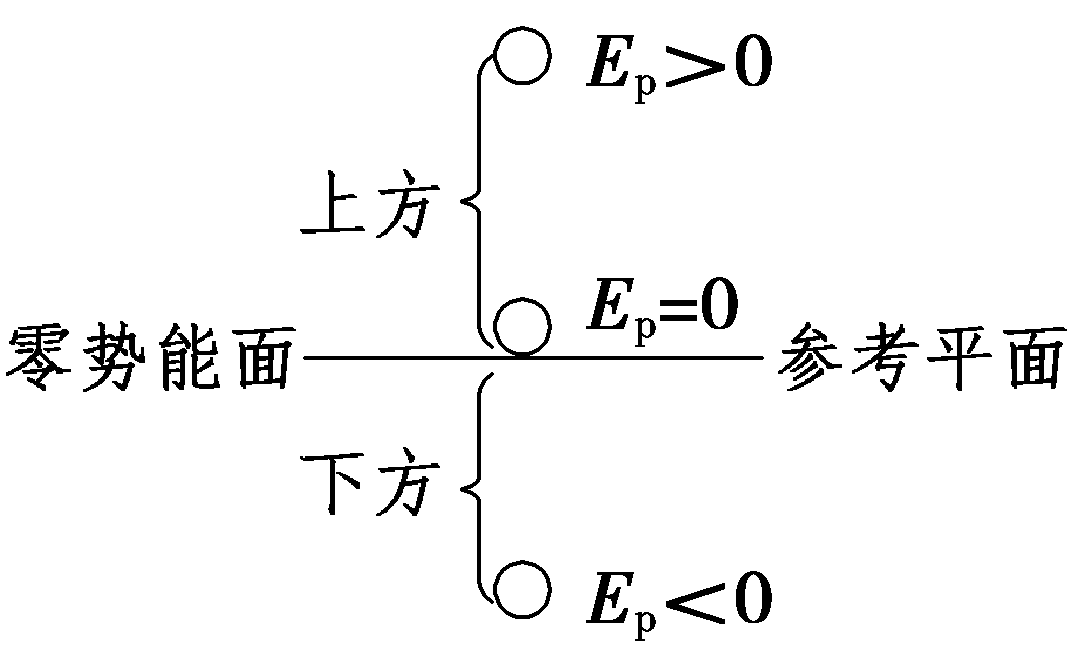
对于选定的参考平面,上方物体的重力势能是正值,下方物体的重力势能是负值,负号表示物体在这个位置具有的重力势能要比在参考平面上具有的重力势能小。
        【二】深化提升
1.重力势能的四个特性
(1)系统性:重力势能是物体和地球组成的系统共同具有的,平时所说的“物体”的重力势能只是一种简化的说法。
(2)相对性:①重力势能E_p＝mgh与参考平面的选择有关,式中的h是物体重心到参考平面的高度
        ②重力势能是标量,只有大小,没有方向,但有正、负之分
        ③物体重力势能的正、负表示是比零势能大还是比零势能小
(3)任意性:参考平面的选取视处理问题的方便而定，一般选择地面或物体运动过程所达到的最低点为参考平面。
(4)绝对性:物体从一个位置运动到另一个位置的过程中，重力势能的变化量与参考平面的选取无关，它的变化量是绝对的。
2.重力势能正、负的理解
要注意重力势能的正、负与功的正、负的区别，重力势能的正、负表示大小，正值比零大，负值比零小，而功的正、负表示是动力做功还是阻力做功。
重力做功与重力势能变化的关系：
(1)关系：W_G＝E_p1－E_p2＝－ΔE_p。
(2)意义：①重力做功的过程就是重力势能改变的过程；
        ②重力做正功，重力势能减少，重力做负功，重力势能增加，且重力做了多少功，重力势能就改变多少。
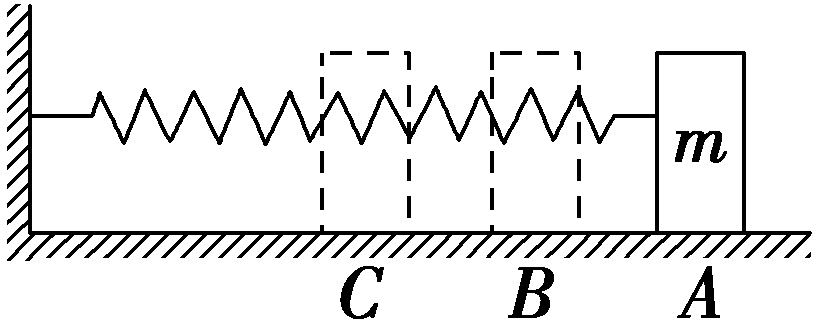
三、弹性势能
        【一】知识梳理
1．弹性势能：发生弹性形变的物体的各部分之间，由于有弹力的相互作用，也具有势能，这种势能叫作弹性势能。
2．弹簧的弹性势能：一般规定，弹簧的长度为原长时，弹性势能为0；弹簧被拉伸或被压缩时，就具有了弹性势能。
3．弹力做功与弹性势能的变化
        弹簧弹力做正功，弹簧的弹性势能减小；弹簧弹力做负功，弹簧的弹性势能增大。
        【二】深化提升
1.对弹性势能的理解
(1)系统性：弹性势能是发生弹性形变的物体上所有质点因相对位置改变而具有的能量，因此弹性势能具有系统性。
(2)弹簧弹性势能的影响因素
①弹簧的形变量x；②弹簧的劲度系数k。
(3)相对性：弹性势能的大小与选定的弹性势能为零的位置有关，对于弹簧，一般规定弹簧处于原长时的弹性势能为零。
2．弹性势能与弹力做功的关系
弹性势能的变化只与弹力做功有关，弹力做负功，弹性势能增大，反之则减小。表达式：W_弹＝－ΔE_p＝E_p1－E_p2。
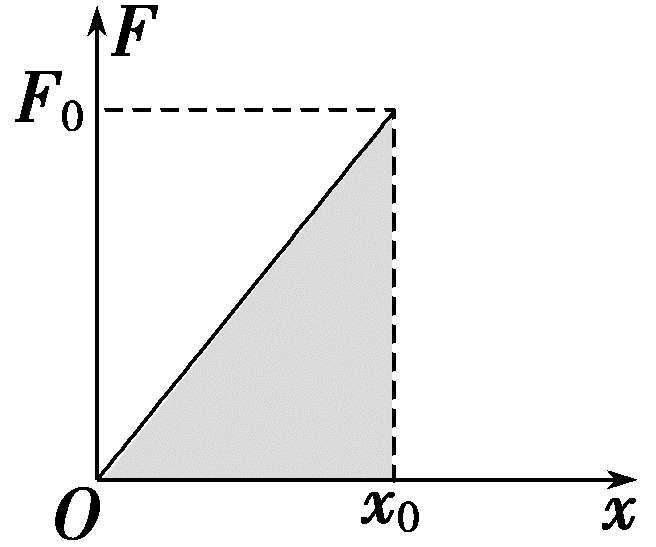
3．弹性势能表达式的推导
根据胡克定律F＝kx，作出弹力F与弹簧形变量x关系的F-x图线，如图所示，根据W＝Fx可知，图线与横轴所围的面积表示F所做的功，即W₀＝(KX₀²)/2＝(kx₀²)/2，由此可知Ep＝(KX²)/2。