1.知道电势差的概念，知道电势差与零电势点的选择无关。2.掌握两点间电势差的表达式，知道两点之间电势差正负的意义。3.知道在电场中移动电荷时静电力做功与两点间电势差的关系，会应用U_AB＝W_AB/q进行相关计算。4.知道等势面的定义，知道电场线一定垂直于等势面。

一、电势差
        【一】知识梳理
1.定义：在电场中，两点之间电势的差值叫作电势差，也叫作电压。
2.公式：设电场中A点的电势为φ_A，B点的电势为φ_B，则它们之间的电势差可以表示为U_AB＝φ_A－φ_B，也可以表示为U_BA＝φ_B－φ_A，所以U_AB＝－U_BA。
3.电势差的正负
电势差是标量，但有正、负。电势差的正、负表示两点电势的高低。所以电场中各点间的电势差可依次用代数法相加。
4.电势差的单位
在国际单位制中，电势差与电势的单位相同，均为伏特，符号是V。
5.静电力做功与电势差的关系
(1)公式推导：电荷q在电场中从A点移到B点时，W_AB＝E_pA－E_pB＝q(φ_A－φ_B)＝qU_AB，所以有U_AB＝W_AB/q。
(2)公式：U_AB＝W_AB/q。
(3)物理意义：电场中A、B两点间的电势差，等于将电荷由A点移至B点的过程中静电力做的功与电荷量q的比值。
        【二】深化提升
1.对电势差的理解
(1)电势差反映了电场的能的性质，决定于电场本身，与试探电荷无关。
(2)电势差可以是正值也可以是负值，电势差的正负表示两点电势的高低，且U_AB＝－U_BA，与零电势点的选取无关。
(3)电场中某点的电势在数值上等于该点与零电势点之间的电势差。
2.电势差与电势的比较
(1)电势φ:电势能与电荷量的比值φ＝E_p/q;由电场和在电场中的位置决定；与零电势点的选取有关。
(2)电势差U:静电力做功与电荷量的比值U＝W/q;由电场和场内两点位置决定；与零电势点的选取无关。
(3)联系：
[1]数值关系：U_AB＝φ_A－φ_B，当φ_B＝0时，U_AB＝φ_A。
[2]单位相同，均是伏特(V)。
[3]都是标量，且均具有正负。
[4]物理意义:均是描述电场的能的性质的物理量
3.对公式W_AB＝qU_AB和U_AB＝W_AB/q的理解
(1)公式W_AB＝qU_AB适用于任何电场，计算时要注意W与U的下角标要对应，如W_AB＝qU_AB，W_BA＝qU_BA。
(2)电势差U_AB仅与电场中A、B两点的位置有关，可以利用来计算A、B两点间的电势差。
(3)W_AB、U_AB均可正可负，但代表的意义不同。W_AB取正号，表示静电力做正功，U_AB取正号，表示φ_A＞φ_B；W_AB取负号，表示静电力做负功，U_AB取负号，表示φ_A＜φ_B。
(4)W_AB＝qU_AB中，静电力做的功W_AB与移动电荷q的路径无关，只与初、末位置的电势差有关。
4.静电力做功的四种求法
(1)功的定义:W＝Fd＝qEd;[1]适用于匀强电场,[2]d表示沿电场线方向的距离
(2)功能关系:W_AB＝Ep_A－Ep_B＝－ΔE_p;
(3)电势差法:W_AB＝qU_AB;
(4)动能定理:W_静电力＋W_其他力＝ΔE_k;
(2)(3)(4)[1]既适用于匀强电场也适用于非匀强电场,[2]既适用于只受静电力的情况，也适用于受多种力的情况
二、等势面
        【一】知识梳理
1.定义：电场中，电势相同的各点构成的面。
2.等势面的特点
(1)在同一等势面上移动电荷时，静电力不做功。
(2)电场线跟等势面垂直，并且由电势高的等势面指向电势低的等势面。
(3)两个不同的等势面永不相交。
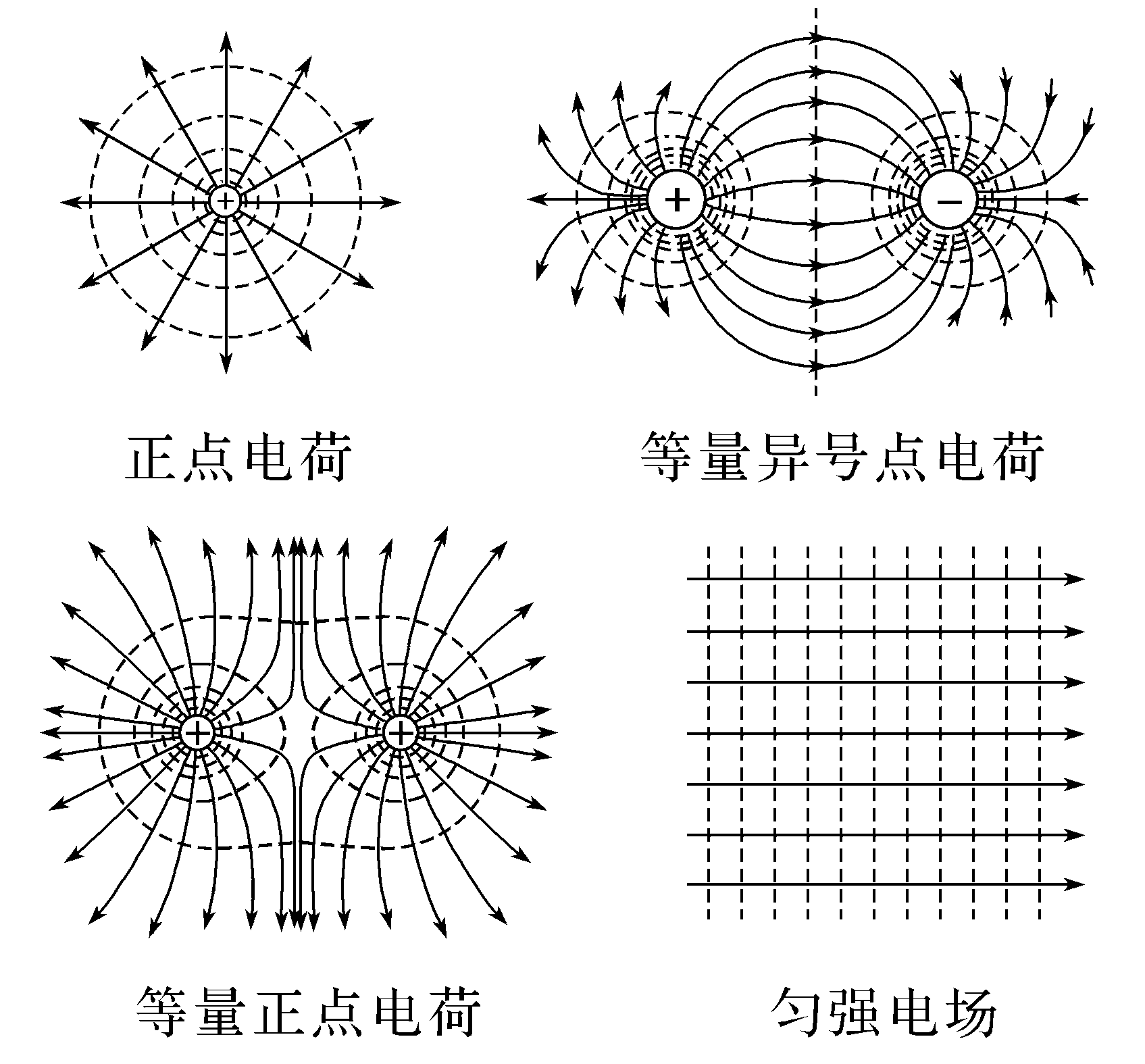
        【二】深化提升
1.几种常见电场的等势面(如图所示)
(1)点电荷的等势面是以点电荷为球心的一簇球面。
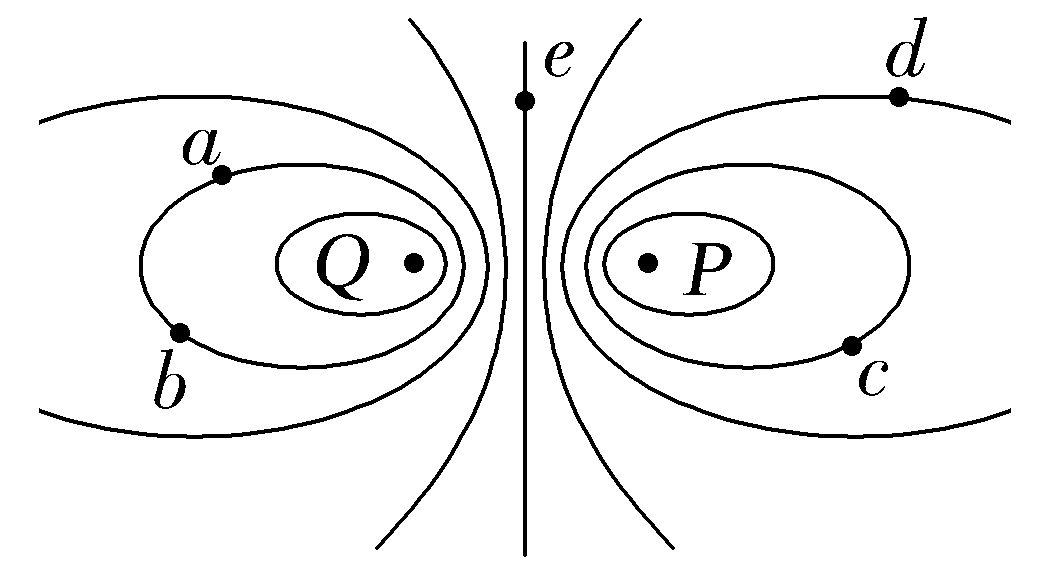
(2)等量异号点电荷的等势面：点电荷的连线上，从正电荷到负电荷电势越来越低，两点电荷连线的中垂线是一条等势线。
(3)等量同号点电荷的等势面
①等量正点电荷连线的中点电势最低，两点电荷连线的中垂线上该点的电势最高，从中点沿中垂线向两侧，电势越来越低。
②等量负点电荷连线的中点电势最高，两点电荷连线的中垂线上该点的电势最低，从中点沿中垂线向两侧，电势越来越高。
(4)匀强电场的等势面是垂直于电场线的一簇平行等间距的平面。
2.等势面的应用
(1)由等势面可以判断电场中各点电势的高低。
(2)由等势面可以判断电荷在电场中移动时静电力做功的情况。
(3)由于等势面和电场线垂直，已知等势面的形状分布，可以绘制电场线，从而确定电场大体分布。
(4)由等差等势面的疏密，可以定性地比较其中两点电场强度的大小。
3.等势面和电场线关系的应用
(1)已知等势面的情况，可作等势面的垂线来确定电场线，并由“电势降低”的方向确定电场线方向。
(2)已知电场线时，可作电场线的垂线来确定等势面，并由“沿电场线方向电势降低”确定等势面的电势高低。